少儿编程网

原文作者：千里马快乐编程

物体旋转涉及到三角函数的知识。推导过程需要一定的篇幅。我们只需要记住简单的结论来应用就可以了。

旋转可以分为三种：沿x轴的旋转、沿y轴的旋转和沿z轴的旋转。

沿x轴旋转时，物体的x坐标不变，y坐标和z坐标的变换规律是(A为旋转角度)：

新的y坐标 = y * cos A + z * sin A

新的z坐标 = z * cos A – y * sin A

沿y轴旋转时，物体的y坐标不变，x坐标和z坐标的变换规律是(A为旋转角度)：

新的x坐标 = x * cos A – z * sin A

新的z坐标 = x * sin A + z * cos A

沿z轴旋转时，物体的z坐标不变，x坐标和y坐标的变换规律是(A为旋转角度)：

新的x坐标 = x * cos A – y * sin A

新的y坐标 = x * sin A + y * cos A

下图显示了沿z轴旋转时的变换情况。有兴趣的同学可以自己推导出坐标的变换规律。

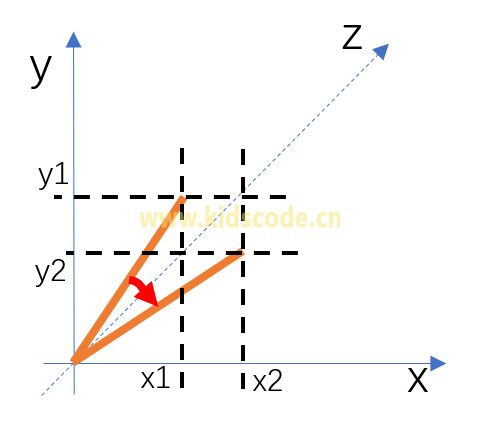
注意上面说的坐标变化都是物体原3D坐标的变化，而不是投射在2D平面上的投射坐标的变化。换言之，旋转改变物体坐标后，还要重新计算投射坐标。

旋转的实现方法：

数字键控制旋转

旋转改变物体坐标后，还要重新计算投射坐标

根据推导的公式，实现坐标改变的具体方法

效果如下：

本站内容未经许可，禁止任何网站及个人进行转载。